浮点数的双精度、单精度和半精度

浮点数是计算机上最常用的数据类型之一，有些语言甚至数值只有浮点型（如Perl，Lua）。常用的浮点数有双精度、单精度和英伟达提出的半精度。双精度和单精度是为了计算，而半精度更多是为了降低数据传输和存储成本。

很多场景对于精度要求也没那么高，例如分布式深度学习里面，如果用半精度的话，比起单精度来可以节省一半传输成本。考虑到深度学习的模型可能会有几亿个参数，使用半精度传输还是非常有价值的。

双精度64位，单精度32位，半精度16位。Google的TensorFlow也使用16位的浮点数（bfloat16），但与英伟达标准不同的是，TensorFlow直接把32位的浮点数小数部分截掉，直接节省一半的储存空间和带宽。

比较下几种浮点数的layout:

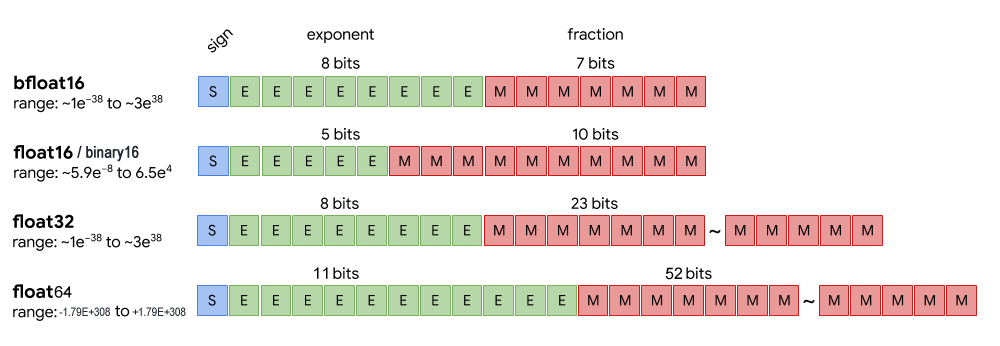
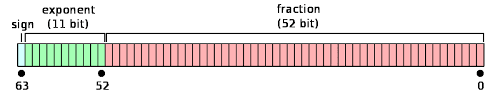
它们都分成3部分，符号位，指数和尾数。不同精度只不过是指数位和尾数位的长度不一样。

解析一个浮点数就5条规则

如果指数位全零，尾数位是全零，那就表示0；
如果指数位全零，尾数位是非零，就表示一个很小的数（subnormal），计算方式 (−1)^signbit × 2^−126 × 0.fractionbits；
如果指数位全是1，尾数位是全零，表示正负无穷；
如果指数位全是1，尾数位是非零，表示不是一个数NAN；
剩下的计算方式为 (−1)^signbit × 2^(exponentbits−127) × 1.fractionbits。

常用的语言几乎都不提供半精度的浮点数，这时候需要我们自己转化。

双精度浮点数，单精度浮点数和半精度浮点数对应不同的计算能力，如双精度用于生化物理研究模拟等高精度科学计算，单精度对应普通影音处理，而半精度可用于AI的深度学习和机器学习 (ML) ，研究表明，许多机器学习模型可容许较低精度的算法而不降低收敛准确性。