数理统计（英语：Mathematical statistics）是统计学的数学基础，从数学的角度去研究统计学，为各种应用统计学提供理论支持。

数理统计是将概率论（数学的一个分支）应用于统计，而不是用于收集统计数据的技术。用于此目的的特定数学技术包括数学分析，线性代数，随机分析，微分方程和测度理论。

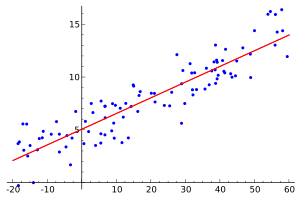
数据集上的线性回归图。回归分析是数理统计的重要部分

简介

统计数据收集与研究计划有关，特别是与随机实验的设计以及使用随机抽样的调查计划有关。数据的初始分析通常遵循进行研究之前指定的研究方案。还可以对研究数据进行分析，以考虑受初始结果启发的次要假设，或提出新的研究建议。计划研究的数据的辅助分析使用了数据分析的工具，而这样做的过程是数学统计。

数据分析分为：

• 描述性统计 -描述数据的统计部分，即概述数据及其典型属性。
• 推论统计 -从数据得出结论的统计部分（使用某种数据模型）：例如，推论统计包括选择数据模型，检查数据是否满足特定模型的条件以及量化涉及不确定性（例如使用置信区间）。

尽管数据分析工具最适用于随机研究的数据，但它们也适用于其他类型的数据。例如，根据自然实验和观察研究，在这种情况下，推断取决于统计学家选择的模型，因此是主观的。

重要主题：

概率分布

甲概率分布是一个函数指派一个概率给每个可测量子集的随机的可能结果的实验，调查，或过程的统计推断。在样本空间为非数值的实验中可以找到示例，其中的分布将是分类分布。样本空间由离散随机变量编码的实验，其中的分布可以由概率质量函数指定; 以及使用由连续随机变量编码的样本空间进行的实验，其中的分布可以由概率密度函数指定。更复杂的实验，例如那些涉及连续时间定义的随机过程的实验，可能需要使用更一般的概率测度。

概率分布可以是单变量或多变量。单变量分布给出单个随机变量采用各种替代值的概率；多元分布（联合概率分布）给出采用各种值组合的随机向量（两个或多个随机变量的集合）的概率。重要且常见的单变量概率分布包括二项式分布，超几何分布和正态分布。该多元正态分布 是常见的多元分布。

特殊发行

• 正态分布，最常见的连续分布
• 伯努利分布，针对单个伯努利试验的结果（例如成功/失败，是/否）
• 二项分布，对于给定的固定独立发生总数，“正发生”的数目（例如成功，赞成票等）
• 负二项分布，用于二项式观察，但其中关注的数量是在给定成功次数之前发生的失败次数
• 几何分布，用于二项式观测，但是关注的数量是首次成功之前的失败数量；负二项式分布的一种特殊情况，成功次数为1。
• 离散的均匀分布，用于有限的一组值（例如，公平死亡的结果）
• 连续均匀分布，用于连续分布的值
• 泊松分布，对于给定时间段内泊松型事件的发生次数
• 在下一次泊松型事件发生之前的时间内的指数分布
• Gamma分布，表示接下来的k个Poisson型事件发生之前的时间
• 卡方分布，标准正态变量平方和的分布；有用，例如，用于推断正态分布样本的样本方差（请参见卡方检验）
• 学生t分布，标准正态变量与比例卡方变量的平方根之比的分布; 对于关于推理有用平均正常分布的样本与未知的方差（见学生t检验）
• Beta分布，具有单个概率（0到1之间的实数）；与伯努利分布和二项式分布共轭

统计推断

统计推断是从数据中得出结论的过程，这些数据可能会发生随机变化，例如观察误差或采样变化。这种推理和归纳程序系统的最初要求是，该系统在应用于定义明确的情况时应产生合理的答案，并且应具有足够的通用性以适用于各种情况。推论统计用于检验假设并使用样本数据进行估计。而描述性统计描述的样本，推断统计推断人口较多的样品能代表预测。

统计推断的结果可能是对“下一步应该做什么？”这个问题的答案，这可能是做出进一步实验或调查的决定，或者是在实施某些组织或政府政策之前得出结论的决定。在大多数情况下，统计推断使用有关人群的命题，这些数据是通过某种形式的随机抽样从感兴趣人群中得出的。更一般而言，有关随机过程的数据是从有限时间内观察到的行为获得的。给定一个参数或假设，希望进行推断，统计推断最常​​使用：

• 当使用随机化时，已知应该生成数据的随机过程的统计模型，以及
• 随机过程的特定实现；即一组数据。

回归分析

在统计中，回归分析是用于估计变量之间关系的统计过程。当关注于因变量和一个或多个自变量之间的关系时，它包括许多用于建模和分析多个变量的技术。更具体地说，回归分析可帮助人们理解，当任何一个自变量发生变化而其他自变量保持固定时，因变量（或“标准变量”）的典型值将如何变化。最常见的是，回归分析会在给定自变量（即平均值）的情况下估算因变量的条件期望自变量固定时因变量的大小。较不常见的是，焦点放在给定自变量的因变量条件分布的分位数或其他位置参数上。在所有情况下，评估对象是一个函数调用的自变量的回归函数。在回归分析中，表征因变量围绕回归函数的变化也很有趣，这可以用概率分布来描述。

已经开发出许多用于进行回归分析的技术。熟悉的方法（例如线性回归）是参数化的，因为回归函数是根据从数据（例如，使用普通最小二乘法）估计的有限数量的未知参数来定义的。非参数回归是指允许回归函数位于一组特定函数中的技术，这些函数可以是无限维的。

非参数统计

非参数统计是从数据中计算出的值，该值不是基于参数化的概率分布族。它们包括描述性统计和推论统计。典型的参数是平均值，方差等。与参数统计不同，非参数统计不对要评估的变量的概率分布做出任何假设。

非参数方法广泛用于研究按顺序排列的人群（例如获得一到四颗星的电影评论）。当数据具有排名但没有明确的数字解释时，例如在评估偏好时，可能需要使用非参数方法。就测量水平而言，非参数方法会得出“常规”数据。

由于非参数方法的假设较少，因此它们的适用性比相应的参数方法要广泛得多。特别是，它们可以应用在对所涉及的应用知之甚少的情况下。而且，由于依赖较少的假设，因此非参数方法更加健壮。

使用非参数方法的另一个理由是简单性。在某些情况下，即使合理使用参数方法，非参数方法也可能更易于使用。由于这种简单性和更高的鲁棒性，一些统计学家认为非参数方法为不当使用和误解留出了更少的空间。

统计，数学和数学统计

数理统计是学科的一个重要子集的统计数据。统计理论家使用数学研究和改进统计程序，而统计研究通常会提出数学问题。统计理论依赖于概率和决策理论。

高斯（Gauss），拉普拉斯（Laplace）和CS皮尔斯（CS Peirce）等数学家和统计学家使用具有概率分布和损失函数（或效用函数）的决策理论。亚伯拉罕·瓦尔德（Abraham Wald）及其继任者重新激发了决策理论的统计推断方法，并广泛使用了科学计算，分析和优化方法 ; 为了设计实验，统计人员使用代数与组合学。

数理统计学的职业前景

统计学是应用数学的分支，这个专业的就业情景比较乐观，一直以来吸引着大批的申请者。学生如果要申请统计学专业，除了需要有良好的数学基础，还需要学习统计分析软件的使用方法。

虽然统计学从属于数学类，但是从北美大学的设置来看，统计已经慢慢从数学系中独立出来，成为单独的统计系。数理统计学是一门研究有效地运用数据收集与数据处理、应用广泛的基础性学科。这个专业一般被人认为是硬科学，学起来不是很容易，需要具备扎实的数学基础。